Hejsan, i det här inlägget tänkte vi berätta om ett väldigt användbart och häftigt räknetrick för att hjälpa huvudräkningen på traven, som vi upptäckte när vi läste igenom Matematik 2b kurslitteratur för gymnasiet.
Tricket är speciellt effektivt när du får två tal som skall multipliceras, som består av 10 i värde eller mer. T ex. talen 17 och 27 – Att memorera in multiplikationstabeller så här pass högt tror jag inte det är många som gör, och det är här huvudräkningstricket kommer in i bilden. Det enda tricket kräver är eventuellt en penna och papper.
Första steget handlar om att göra multiplikationen enklare för oss genom att dela upp våra två tal i mindre beståndsdelar som kan adderas med varandra för att bilda de talen vi hade i vår multiplikation. Så i vårt fall hade vi talen 17 och 27, om vi börjar med talet 17 så kan vi se med enkelhet att vi kan få talet 17 genom att ta 10 + 7, på samma sätt kan vi med enkelhet se att talet 27 kan vi få genom att ta 20 + 7.
Med denna kunskap kan vi då ställa upp följande uträkning:
(10+7)(20+7)
Och sedan kan vi nyttja multiplikationsregeln mellan två parenteser som vardera innehåller två eller flera tal, som fungerar på följande vis:
- 10*20 = 200 (första termen i första parentesen multiplicerades in med första termen i andra parentesen)
- 10*7 = 70 (första termen i första parentesen multiplicerades in med andra termen i andra parentesen)
- 7*20 = 140 (andra termen i första parentesen multiplicerades in med första termen i andra parentesen)
- 7*7= 49 (andra termen i första parentesen multiplicerades in med andra termen i andra parentesen)
- Slutligen adderar vi samman alla resultat vi fått: 200+70+140+49 och får svaret: 459.
För er som tycker en bild hade underlättat den kanske något röriga förklaringen ovan, se nedan:
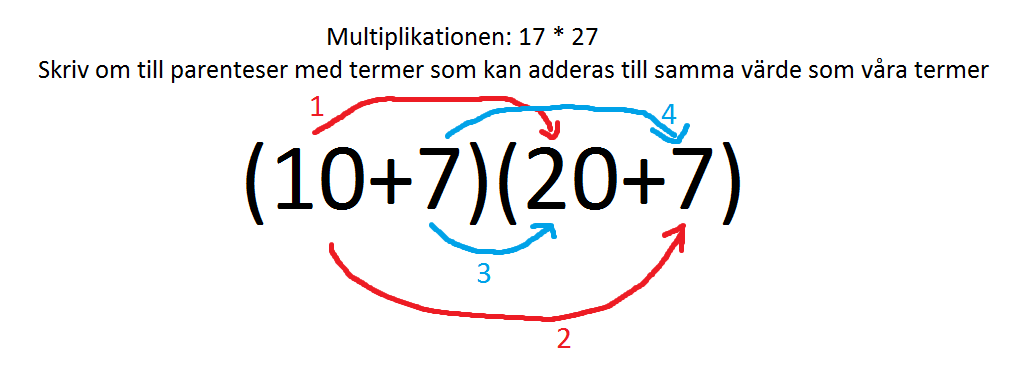
Och som ni säkert märkte av tillvägagångssättet att räkna Multiplikation med högre tal på det här viset, så underlättade det en hel del – och kan vara ett smart alternativ att sätta sig in i och lära sig för de tillfälle då en räknare inte får användas.
Ytterligare en grej man kan göra då man har höga tal multiplicerade med sig själva (eller upphöjt med 2) – är att man man istället kan skriva upp det på följande vis för t ex. \( 52^2 \):
\[ (50+2)^2 = 50^2+2^2+2*50*2=2500+4+200=2704 \]