Detta är vårt tredje inlägg om Bråkräkning och även detta bygger på föregående inlägg: Addition med Bråk, såväl som Subtraktion med Bråk.
Men som tidigare inlägg, täcker vi även i detta inlägg ett nytt räknesätt – nämligen Multiplikation med bråktal.
Multiplikationen med bråk skiljer sig lite från hur vi räknade Addition och Subtraktion med bråktal, på det sätt att man inte längre behöver oroa sig för MGN på samma sätt, eller förlängning av bråk och sedan skriver man även samman de två bråktalen man räknar med på ett gemensamt bråkstreck och förkortar bråken korsvis (snett) innan man räknar ut svaret. Se exempel nedan:
\[ \frac{3}{4}*\frac{8}{9} = \frac{3*8}{4*9}=\frac{1*2}{1*3}=\frac{2}{3} \]
Som ni då kan se ovan så satt vi täljarna med multiplikation ovanför bråkstrecket, medan vi satt nämnarna under bråkstrecket – även dem med multiplikation emellan.
Sedan när vi kom till det gemensamma bråkstrecket så förkortade vi Första bråktalets Täljare med Andra bråktalets Nämnare och vice-versa så även Andra bråktalets Täljare förkortades med Första bråktalets Nämnare – Så t ex. 3:an och 9:an förkortades och 3:an gick 3 gånger i 9, vilket gav oss en 3:a där 9:an satt (9/3 = 3), medan 3:an vi hade från början ersattes av en 1:a (3/3 = 1). Samma sak gjordes sen för 8:an och 4:an (8/4 = 2 och 4/4 = 1).
Så om vi skulle dela upp Multiplikation med bråk processen i steg hade första steget varit att sätta gemensamt bråkstreck för att sedan i andra steget korsvis förkorta bråktalen innan vi löste ut slutliga svaret.
För er som fortfarande hade lite svårt att hänga med i hur korsvis förkortningen fungerade, se illustrationen nedan:
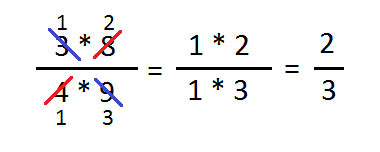
Detta sätt att skriva brukar också vara godtagbart för de flesta lärare om ni ska lösa sådan uppgift på prov eller liknande – är ni osäkra, så fråga er lärare vad som gäller. Sättet att skriva (tycker jag åtminstone) illustrerar på ett bra och enkelt vis hur man har tänkt! Vilket är viktigt både för dig själv såväl som dina lärare.