Detta blir vårt fjärde och näst-sista inlägg för Bråkräkning såhär långt, även detta kommer baseras mycket på tidigare inlägg: Addition med Bråk, Subtraktion med Bråk samt- men speciellt: Multiplikation med Bråk!
Vad är då anledningen att vi säger speciellt Multiplikation med Bråk? Jo, Division med Bråk samt Multiplikation med Bråk har mycket gemensamt – såsom: Skrivsättet Gemensamt bråkstreck, såväl som Korsvis förkortning innan slutlig lösning. Och Division med Bråk varken förlänger eller behöver hitta MGN för bråktalen man ska räkna med – precis som för Multiplikation med Bråk. Exempel på hur division med bråk kan skrivas kan ni se nedan:
\[ \frac{3}{7}/\frac{9}{21}:ELLER:\frac{\frac{3}{7}}{\frac{9}{21}} \]
Som ni kan se ovan kan division mellan två bråk skrivas på två olika sätt. Båda sätten att skriva det på betyder samma sak! Dock personligen föredrar jag själv det första skrivsättet då det ”känns lättare” att räkna med med tanke på steget innan Gemensamt bråkstreck för Division med Bråk som vi beskriver och förklarar i stycket nedan.
Division med Bråk skiljer sig lite från Multiplikation med Bråk på så sätt att där finns ytterligare en teknik att använda innan man skapar det Gemensamma bråkstrecket med de båda bråktalen. Denna teknik kallas invertering och går ut på att vi ”vänder upp-och-ned” på det andra bråktalets Täljare och Nämnare så att bråktalets Täljare blir Nämnare och vice-versa. Nedan visar vi exempel på detta:
\[ \frac{3}{7}/\frac{9}{21}=\frac{3*21}{7*9}=\frac{1*3}{1*3}=\frac{3}{3}=1 \]
Notera: att vi fortfarande Korsvis förkortar efter vi har ställt upp det på det Gemensamma bråkstrecket och innan vi löser ut slutliga svaret.
Personligen föredrar jag det skrivsätt där ett snedstreck (/) separerar bråktalen, då invertering känns enklare att förstå sig på då man enkelt bara vänder upp-och-ned på andra bråktalets Täljare och Nämnare så deras värden byter plats. En enklare illustration som visar hur man kan föreställa sig vad man gör:
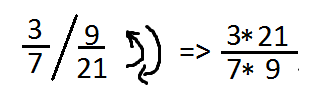
För många kan Division med Bråk kännas klurigare och svårare än de andra räknesätten med Bråk, detta är förståeligt då invertering kan kännas främmande för många i början- men förhoppningsvis hjälper det vi skrivit i det här inlägget för att hjälpa er få förståelse för det hela lite bättre.
Vi önskar er Lycka till med framtida bråkräkning!