Jag minns själv att Bråk var något av det som tog längst tid för mig personligen att få full förståelse för, men efter att man hade fått förståelse för det så var det precis som en helt ny värld öppnade sig. Helt plötsligt blev uträkningar som annars tog lång tid och gav huvudvärk lika enkla som addition och subtraktion.
Bråkräkning är definitivt ett av de kraftfullaste sätten att hantera tal i matematiken då de på ett väldigt perfekt och kanske mer tydligt sätt representerar tal i jämförelse med t ex. decimaltal som ofta får avrundas – och även när de inte avrundas är de inte alltid roliga att räkna med.
Så jag tänkte börja med att gå igenom addition av bråk i detta inlägg, för att sparka igång bråkräkningen för oss.
Men innan vi börjar med addition i bråkräkning överhuvudtaget tänkte jag ge en kort introduktion till terminologi för bråkräkning.
\[ \frac{Täljare}{Nämnare} \]
Det ni ser ovan är vad de olika termerna för ett bråk kallas (samma som för division) – talet ovanför bråkstrecket är vår Täljare, medan talet under vårt bråkstreck är vår Nämnare.
När vi räknar med bråk i addition kan det vara så enkelt som:
\[ \frac{1}{2} + \frac{1}{2} = \frac{2}{2} = 1 \]
Skulle vi översätta ovan bråkräkning i decimaltal så hade det sett ut såhär:
\[ 0.5 + 0.5 =1 \]
Och ibland kan decimaltal vara att föredra att använda vid specifika uträkningar, men ibland är faktiskt bråkräkning betydligt bättre, enklare och snabbare!
Tyvärr är det inte alltid så enkelt som ovan exempel dock, ibland får vi addition med bråk som ser ut såhär:
\[ \frac{1}{3}+\frac{1}{4}=? \]
Motsvarighet i decimaltal är:
\[ 0.333… + 0.25 = 0.5833… \]
När vi får en sådan uträkning kan vi inte bara lägga ihop Täljarna som vi gjorde för additionen av bråk med samma Nämnare, och vi kan inte göra detta då bråktal med olika Nämnare har olika värde(!) och att lägga ihop tal med olika värde hade helt enkelt inte gått.
Vad vi då måste göra är att ta reda på en Minsta Gemensamma Nämnare (MGN) som de båda bråktalen har gemensamt.
Ett snabbt sätt att göra detta på, hade varit att Multiplicera Nämnarna med varandra dock är det inte alltid detta ger oss den Minsta gemensamma Nämnaren. Ofta när vi har att göra med så pass små Nämnare som i våra bråktal ovan, är det hyfsat enkelt att se Nämnare som de båda har gemensamt genom att ha god kännedom om Multiplikationstabellen.
I vårt fall ovan, hade vi 1/3 och 1/4 – tittar vi på nämnarna 3 och 4 så kan vi se att vår Minsta Gemensamma Nämnare blir 12 – då både 3 multiplicerat (förlängt) med något tal kan bli 12, och likaså kan vår 4:a.
Vi får då:
\[ \frac{1}{3}+\frac{1}{4}=\frac{1*4}{3*4}+\frac{1*3}{4*3}=\frac{4}{12}+\frac{3}{12}=\frac{7}{12} \]
Ovan kan ni då se hur förlängning av bråk går till och det används för att göra om bråktal med olika Nämnare till bråktal med samma Nämnare – en Minsta Gemensamma Nämnare.
Som ni också kan se av ovan svar från vår bråkräkning efter vi förlängt våra bråk så delade båda en Minsta Gemensam Nämnare. I bråkräkning fick vi 7/12, medan decimaltals räkningsmotsvarigheten ovan gav oss ett väldigt inexakt svar: 0.58333… i jämförelse. Därför är bråkräkning att föredra i de här fallen, du kan skriva in 7/12 i en miniräknare och få ett korrekt o-avrundat svar att jobba med (med alla värdesiffror intakta), jämfört med ett kanske annars avrundat svar där du förlorar en massa värdesiffror som kanske gör enorm skillnad i viktiga uträkningar – trots avrundningens till synes minimala inverkan!
Notera att då vi förlänger både Täljare såväl som Nämnare för att nå MGN i vår addition med bråk ovan, detta innebär att vår förlängning är av samma värde som talet 1 vilket innebär att vi inte förändrar vårt ursprungliga värde – vilket är varför och hur förlängning i bråk funkar, då ursprungliga värden förblir oförändrade, se illustration nedan:
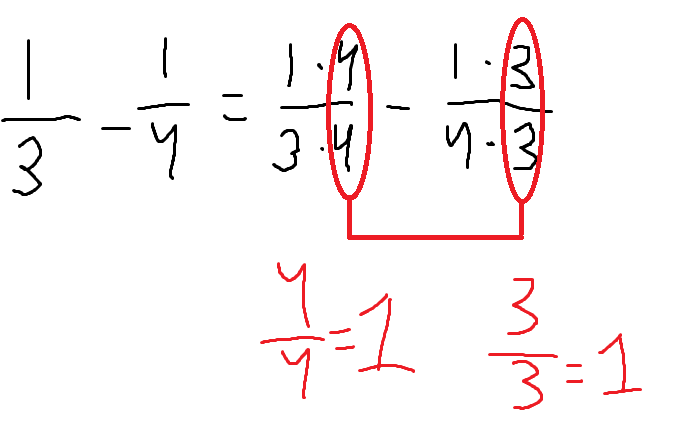
Så oavsett hur stora våra täljare och nämnare blir efter vi förlängt vårt ursprungliga bråk kommer värdet alltid förbli desamma!